Implementation and Math

Complex convolutional networks provide the benefit of explicitly modelling the phase space of physical systems [TBZ+17]. The complex convolution introduced can be explicitly implemented as convolutions of the real and complex components of both kernels and the data. A complex-valued data matrix in cartesian notation is defined as \(\textbf{M} = M_\Re + i M_\Im\) and equally, the complex-valued convolutional kernel is defined as \(\textbf{K} = K_\Re + i K_\Im\). The individual coefficients \((M_\Re, M_\Im, K_\Re, K_\Im)\) are real-valued matrices, considering vectors are special cases of matrices with one of two dimensions being one.

Complex Convolution Math

The math for complex convolutional networks is similar to real-valued convolutions, with real-valued convolutions being:

\[\int f(y)\cdot g(x-y) \, dy\]

which generalizes to complex-valued function on \(\mathbf{R}^d\):

\[(f * g )(x) = \int_{\mathbf{R}^d} f(y)g(x-y)\,dy = \int_{\mathbf{R}^d} f(x-y)g(y)\,dy,\]

in order for the integral to exist, f and g need to decay sufficiently rapidly at infinity [CC-BY-SA Wiki].

Implementation

Solving the convolution of, implemented by [TBZ+17], translated to keras in [DC19]

Complex Convolution implementation (CC-BY [TBZ+17])

\[M' = K * M = (M_\Re + i M_\Im) * (K_\Re + i K_\Im),\]

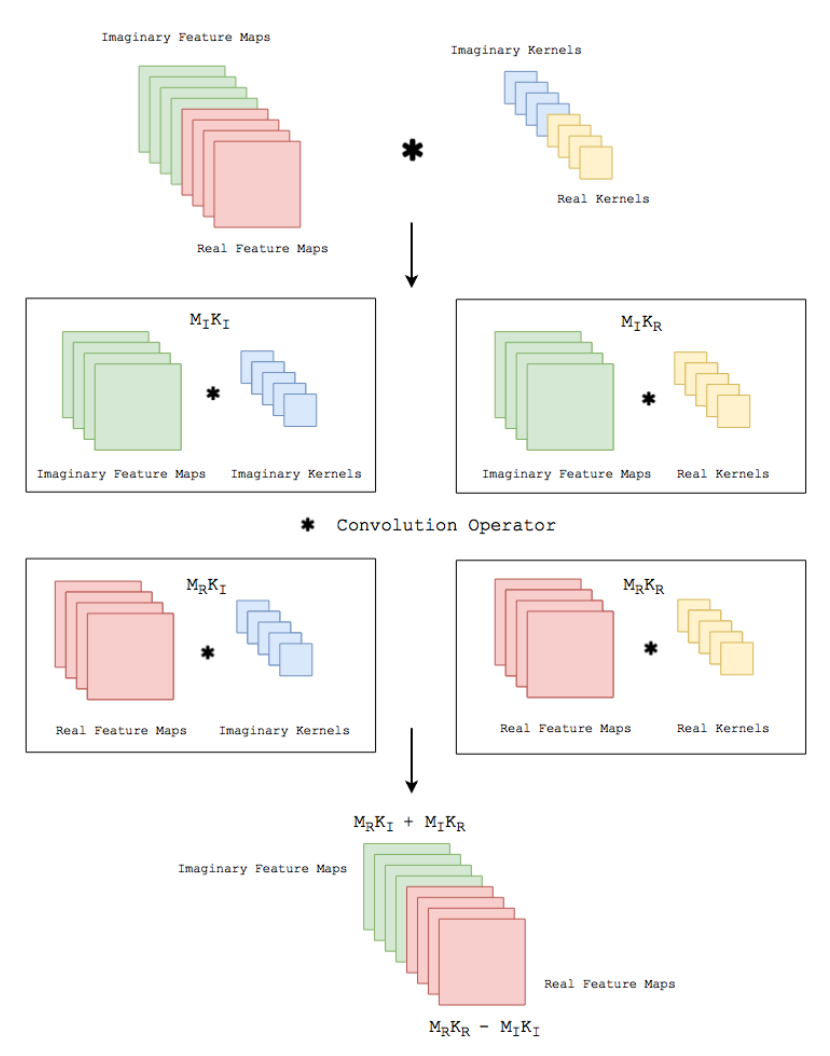
we can apply the distributivity of convolutions to obtain

\[M' = \{M_\Re * K_\Re - M_\Im * K_\Im\} + i \{ M_\Re * K_\Im + M_\Im * K_\Re\},\]

where K is the Kernel and M is a data vector.

Considerations

Complex convolutional neural networks learn by back-propagation. [SSC15] state that the activation functions, as well as the loss function must be complex differentiable (holomorphic). [TBZ+17] suggest that employing complex losses and activation functions is valid for speed, however, refers that [HY12] show that complex-valued networks can be optimized individually with real-valued loss functions and contain piecewise real-valued activations. We reimplement the code [TBZ+17] provides in keras with tensorflow , which provides convenience functions implementing a multitude of real-valued loss functions and activations.

[CC-BY [DLuthjeC19]]

DC19

Jesper Soeren Dramsch and Contributors. Complex-valued neural networks in keras with tensorflow. 2019. URL: https://figshare.com/articles/Complex-Valued_Neural_Networks_in_Keras_with_Tensorflow/9783773/1, doi:10.6084/m9.figshare.9783773.

DLuthjeC19

Jesper Sören Dramsch, Mikael Lüthje, and Anders Nymark Christensen. Complex-valued neural networks for machine learning on non-stationary physical data. arXiv preprint arXiv:1905.12321, 2019.

HY12

Akira Hirose and Shotaro Yoshida. Generalization characteristics of complex-valued feedforward neural networks in relation to signal coherence. IEEE Transactions on Neural Networks and Learning Systems, 2012.

SSC15

Andy M. Sarroff, Victor Shepardson, and Michael A. Casey. Learning representations using complex-valued nets. CoRR, 2015. URL: http://arxiv.org/abs/1511.06351, arXiv:1511.06351.

TBZ+17(1,2,3,4,5)

Chiheb Trabelsi, Olexa Bilaniuk, Ying Zhang, Dmitriy Serdyuk, Sandeep Subramanian, João Felipe Santos, Soroush Mehri, Negar Rostamzadeh, Yoshua Bengio, and Christopher J Pal. Deep complex networks. arXiv preprint arXiv:1705.09792, 2017.